En la corrección de ejercicios es común encontrar confusiones y erratas. Por desgracia, también equivocaciones que dan mucho donde pensar. Pongamos un ejemplo:

Está claro que el alumno se encontró con una gran dificultad al abordad $\log(\tan(px))$, decidiéndose por comprender $\tan(px)$ como un producto de $\tan$ por $px$, de ahí que aplique la propiedad de los logaritmos par el producto:
$$\log(\tan(px))=\log(\tan)+\log(px)$$
Pero como $\log(\tan)$ le sonaba raro decide introducir la $x$ y así dar sentido a la expresión
$$\log(\tan(px))=\log(\tan x)+\log(px).$$
Ahora parece hasta lógica.
Otro alumno optó por modificar $\tan$ para que su significado fuese más claro:
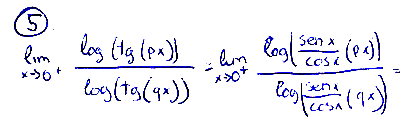
De este modo la complejidad del $\tan$ se solventa al sustituir $\tan=\frac{\sin x}{\cos x}$. Puesto a contar con esta obviedad, el resto conlleva otras más livianas, dentro de la premisa: si la primera es muy gorda y pasa, por el resto no hay que preocuparse.
Como he dicho: mucho que pensar.