Una ecuación diferencial de la forma $$y’+a(x)y=b(x)y^n$$ se denomina ecuación de Bernoulli. Hace referencia al mayor de los Bernoulli, Jakob(1654-1705), de cuya familia tenemos amplios conocimientos en las matemáticas. Jakob la mostró en 1695 en «Explicationes, Annotationes & Additiones ad ea, quae in Actis sup. anni de Curva Elastica, Isochrona Paracentrica, & Velaria, hinc inde memorata, & paratim controversa legundur; ubi de Linea mediarum directionum, alliisque novis», Acta Eruditorum.
Un curiosidad de esta ecuación es que si $n>1$ podemos considerar $z=y^{1-n}$, resulta $z’=-\frac{n-1}{y^n}y’$, y la ecuación anterior se puede expresar como $$z’+(1-n)a(x)z=(1-n)b(x),$$ una ecuación diferencial lineal.
Esta sustitución se le ocurrió a Leibniz, mentor de los hermanos Jakob y Johann(quien también la había resuelto, pero por otro método), en 1696. El inconveniente es que eliminamos las solución singular $y=0$, pero teniéndolo en cuenta podemos utilizar este método.
Por ejemplo en el siguiente problema: El modelo de crecimiento de von Bertalanffy, plantea un modelo matemático de la población de peces, en concreto la predicción del crecimiento de un tipo de pez: $$\frac{dW}{dt}=\alpha W^{\frac{2}{3}}-\beta W,$$ donde $W=W(t)$ representa el peso del un pez, y $\alpha$ y $\beta$ son constantes positivas.
Como el problema presenta una ecuación de Bernoulli, podemos resolver fácilmente preguntas del tipo: la solución general de la ecuación, el peso límite del pez ($W_\infty=\lim_{t\to\infty}W(t)$), o una solución para el problema de valor inicial $W(0)=0$. Como veis, una potente herramienta.
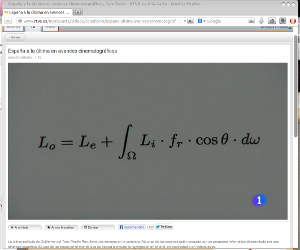


 Los libros de Stewart son muy buenos, en particular los de Calculus ofrecen a los estudiantes de ingenierías de primero de universidad o preuniversitarios, los conocimientos necesarios y suficientes para llevar las asignaturas de cálculo con facilidad. Facilidad dentro de lo condensado del temario y la escasa dedicación que dejan los créditos actuales. Nos quejamos del deficiente nivel en matemáticas que traen nuestros alumnos, al tiempo que los créditos de matemáticas en las ingenierías bajan como la espuma: incongruencias típicas del momento en que vivimos.
Los libros de Stewart son muy buenos, en particular los de Calculus ofrecen a los estudiantes de ingenierías de primero de universidad o preuniversitarios, los conocimientos necesarios y suficientes para llevar las asignaturas de cálculo con facilidad. Facilidad dentro de lo condensado del temario y la escasa dedicación que dejan los créditos actuales. Nos quejamos del deficiente nivel en matemáticas que traen nuestros alumnos, al tiempo que los créditos de matemáticas en las ingenierías bajan como la espuma: incongruencias típicas del momento en que vivimos.