Eratóstenes (Cirene, 276 a. C. – Alejandría, 194 a. C.), fue un célebre matemático, astrónomo y geógrafo griego, que desarrolló gran parte de su trabajo en el egipto de la dinastía Ptolemaica. Esta fue la época de la construcción de la mítica biblioteca de Alejandría, de la cual se hizo cargo en 236 a.C. hasta el fin de sus días.
Se le conoce, principalmente, por el calculo y su precisión de la longitud de la circunferencia de la Tierra. Para ello se sirvió de una ingeniosa idea. Tenía conocimiento de una característica que acontecía todos los solsticios de verano en la localidad de Siena (actual Asuán) en Egipto. Ese día las palmeras no daban sombra lateral y la luz iluminaba el fondo de los pozos. Esto significaba que la luz incidía perpendicularmente a la corteza terrestre ese día en ese lugar.
Puesto que en otros lugares si había sombra, esto solo podía deberse a que la superficie de tierra formaba una curvatura. Esta conjetura se basaba en la suposición de que los rayos del Sol eran
paralelos en ambas localidades: Siena y un pueblo relativamente cercano.
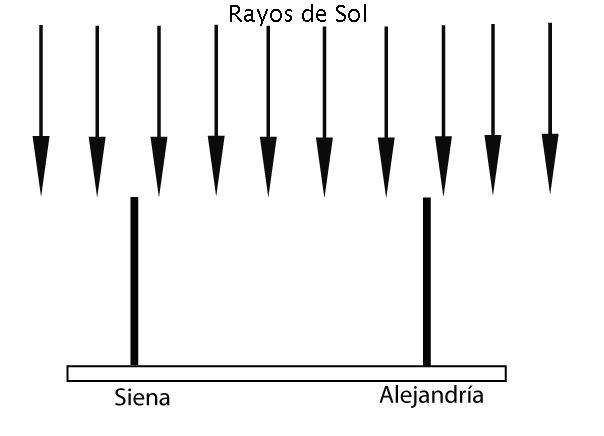
Si la Tierra fuera plana la lejanía del Sol le justificaba para que los rayos incidieran de forma perpendicular en las dos ciudades y provocaría que, por ejemplo, un monolito no ofreciera sombra en el solsticio de verano. Sin embargo, esto no ocurría así.
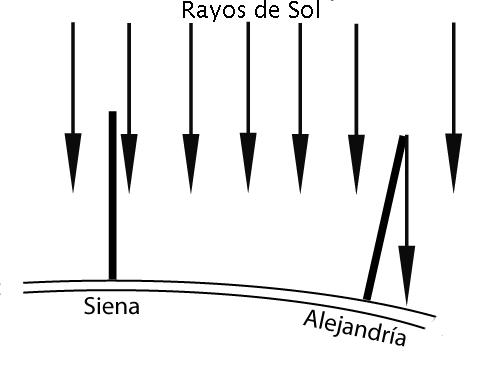
La sombra que proyectaba un monolito de igual dimensión en Alenjandría significaba que la corteza de la tierra era curvada.
Eratóstenes no fue el primero en postular que la Tierra era redonda, ya hubo filósofos griegos como Pitágoras y Aristóteles que la concebían de ese modo. Sin embargo, si fue el primero en intentar determinar su circunferencia.
Sigamos viendo como determinó la longitud. El día del solsticios de verano en Siena los rayos solares caían en línea con un palo clavado perpendicularmente en el suelo. Mientras que, a 4900 estadios de Siena, en Alejandría los rayos paralelos del Sol harían sombra sobre un palo clavado perpendicularmente al suelo.
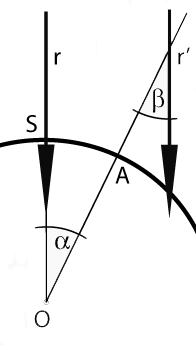
Se refleja la localidad de Siena y A la de Alejandría. r y r’ son los rayos de Sol paralelos que inciden sobre los palos, reflejados por los segmentos extendidos
y
, clavados perpendicularmente en Siena y alejandría respectivamente.
Eratóstenes sabía que la secante que corta dos paralelas produce ángulos iguales, y ,por tanto, los ángulos α y β eran iguales. Calculando el ángulo β obtuvo 7º, lo que significaba que el ángulo α de 7º correspondería a un longitud de arco de 4900 estadios. Ahora solo se necesitaba una regla de tres para determinar la longitud completa de la circunferencia:
![]()
Había calculado la longitud de la circunferencia de la Tierra en 252000 estadios. Los griegos utilizaban como unidad de longitud el estadio, que equivalía a la longitud del estadio de Olimpia, unos 174,125 metros. Sin embargo, en Egipto se utilizaba un estadio de 157,2m, y se cree que la medida empleada por Eratóstenes equivaldría a 158m. Luego sus cálculos obtuvieron una longitud de 39816km y un radio de 6336,89km.
Independientemente del valor del estadio, que nos ofrecería diferencias en los resultados obtenidos bien por exceso o defecto, la aproximación que dio es muy considerable para la época y los medios que disponía.